삼각형 넓이에 관하여

삼각형의 넓이를 구하는 공식은 이미 초등학교에서 배운다. 밑변의 길이가 $a$이고 높이가 $h$인 삼각형 넓이 $A$는

$$A=\frac{1}{2}\times a\times h\tag{1}$$

넓이가 같은 삼각형으로 모양 바꾸기

당연히 밑변과 높이가 서로 같은 삼각형은 넓이가 같다. 이런 성질을 활용하여 우리는 넓이가 같은 삼각형을 쉽게 만들 수 있다. 그림에서 두 직선 $l$과 $m$은 서로 평행하다. 즉, $l//m$. 서로 다른 두 점 $A$와 $B$는 직선 $m$ 위에 있고 두 점 $C$와 $D$는 모두 직선 $l$ 위에 있다고 하자.

그림 1

두 삼각형 $\triangle ABC$와 $\triangle ABD$의 높이는 꼭짓점 $C$와 $D$에서 모두 직선 $m$에 수선의 발을 내려서 찾을 수 있다. $\square CEFD$는 직사각형이므로 $\overline{CE}=\overline{DF}$이다. 따라서 두 삼각형의 넓이는 같다.

$$\frac{1}{2}\times \overline{AB}\times \overline{CE}=\frac{1}{2}\times \overline{AB}\times\overline{DF}$$

넓이가 같음을 기호로는 아래와 같이 적는다.

$$\triangle ABC=\triangle ABD$$

합동 기호 $\equiv$와 혼동하지 말아야 한다.

참고 그림 1에서 직선 $l,m$과 평행한 직선이 삼각형과 만나는 점을 잇는 두 선분 $\overline{PQ}$와 $\overline{RS}$을 생각하자. 닮음을 배웠다면 $\overline{PQ}=\overline{RS}$임을 쉽게 확인할 수 있다. 같은 높이에 있는 선분의 길이가 같으면 두 도형은 넓이가 같다는 카발리에리 원리에 꼭 들어맞는다.

귀찮고 힘들어도 중학생이라면 조금 더 깊이 생각해 보자.

넓이를 측정하는 것은 무엇일까? 길이가 $1$인 선분으로 길이를 재는 것과 마찬가지로 넓이는 한 변의 길이가 $1$인 정사각형의 넓이를 단위로 해서 측정한다. 실제로 우리가 초등학교에서 배운 삼각형의 넓이를 구하는 공식이 따지고 보면 그림에서 설명하는 내용에서 나왔다고 볼 수 있다. 밑변의 길이가 고정되어 있다고 생각하면 꼭짓점을 밑변과 평행한 직선 위를 움직여서 넓이가 같은 직각삼각형을 찾을 수 있다. 

그림 2

합동인 직각삼각형을 붙여서 직사각형을 만들 수 있다. 아래와 같은 직사각형 넓이가 $a\times b$임은 자명하다.

그림 3

아주 옛날 사람들은 그림 3의 직사각형을 반으로 나눈 삼각형을 생각했을 것이다. 그다음에 그림 2를 생각하여 모양이 달라져도 넓이가 달라지지 않음을 알아내고 마침내 공식 (1)을 얻었을 것이다.

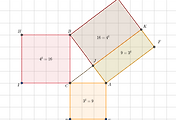
아무튼 유클리드는 이글에서 소개한 삼각형을 같은 넓이를 가진 삼각형으로 변형하는 방법으로 피타고라스 정리를 증명한다.

https://suhak.tistory.com/181

피타고라스 정리의 증명을 몇 가지 알고 있나요?