절대부등식 활용하기

절대부등식은 참임이 증명된 일종의 정리처럼 다른 문제를 풀 때 사용할 수 있다. 

실수 $x, \;y\;$는 $x^2 + y^2 = 9$를 만족한다. $3x + 4y$의 최댓값과 최솟값을 구하고 그때의 실수 $x,y$의 값을 각각 구하시오.

풀이 1 원과 직선의 방정식을 이용한 풀이

원 $x^2 + y^2 = 4$ 위의 점을 지나는 직선 $3x+4y=k$으로 생각할 수 있다. $k$는 원과 직선이 접할 때 최댓값 또는 최솟값을 가진다.

$$\frac{|k|}{\sqrt{3^2 +4^2}}\leq 2$$

$$-10\leq k\leq 10$$

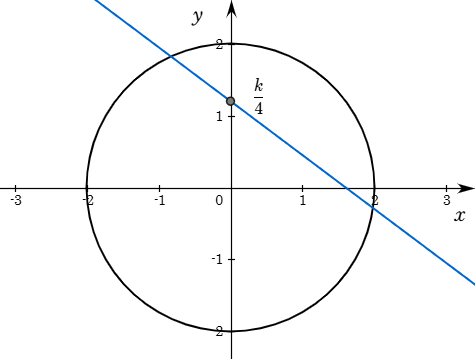
최댓값을 가질 때는 $3x+4y=10$과 원의 교점을 구한다.

$$x=\dfrac{6}{5},\;\;y=\dfrac{8}{5}$$

마찬가지로 최솟값을 가질 때는 $3x+4y=-10$과 원의 교점을 구한다.

$$x=-\dfrac{6}{5},\;\;y=-\dfrac{8}{5}$$

풀이 2 코시-슈바르츠 부등식을 활용한 풀이

아래와 같은 절대부등식을 알고 있다면 조금 더 쉽게 구할 수 있다.

$$(a^2 +b^2)(x^2 +y^2 )\geq (ax+by)^2\tag{1}$$

(1)은 $\dfrac{x}{a}=\dfrac{y}{b}$일 때 등호가 성립한다.

$$(3^2 +4^2)(x^2 +y^2 )\geq (3x+4y)^2$$

$$25\times 5\geq (3x+4y)^2$$

$$\therefore\;\;-10\leq 3x+4y \leq 10$$

$\dfrac{x}{3}=\dfrac{y}{4}=k$라고 놓으면 $k=\pm\dfrac{2}{5}$에서 풀이1과 같은 답을 얻는다.

양수 $x, y$ 에 대하여 식 $(x+y)\left(\dfrac{1}{x} + \dfrac{9}{y}\right)$ 의 최솟값을 구하시오.

아래 (2)와 같은 절대부등식을 활용한다.

$$\frac{a+b}{2}\geq \sqrt {ab}\quad(a>0,\;\;b>0)\tag{2}$$

주어진 식을 전개하자.

$$\begin{split}(x+y)\left(\frac{1}{x} + \frac{9}{y}\right)&=1+\frac{9x}{y}+\frac{y}{x}+9\\&\geq10+2\sqrt{\frac{9x}{y}\times \frac{y}{x}}=16\end{split}$$

등호는 $\dfrac{9x}{y}=\dfrac{y}{x}$일 때 성립한다. $y=3x$일 때 성립한다.